Have you ever wondered about that line stretching from one corner of a square to the opposite corner? That's the diagonal of a square, and understanding it opens up fascinating connections in geometry. Whether you're a student tackling homework, a carpenter planning a project, or just curious about mathematical relationships, our diagonal calculator and this guide will help you master this concept.
What Is a Square?
Before diving into diagonals, let's establish what makes a square special. A square is a four-sided polygon (quadrilateral) with these distinctive properties:
- All four sides have exactly the same length.
- All four interior angles are right angles (90 degrees).
- Opposite sides are parallel to each other.
These properties make the square one of the most perfectly symmetrical shapes in geometry, appearing throughout nature, art, architecture, and engineering.
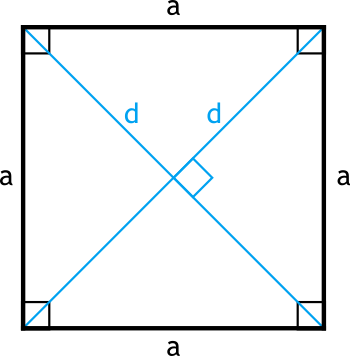
Diagonal of square
The diagonal of a square is a line segment that connects two non-adjacent vertices (corners). Every square has exactly two diagonals, and they intersect at the center of the square.
These diagonals have several important properties:
- Both diagonals of a square have exactly the same length.
- The diagonals bisect each other, meaning they divide each other into two equal parts where they cross.
- The diagonals intersect at right angles (90 degrees).
- Each diagonal divides the square into two equal right triangles.
- The diagonals of a square serve as lines of symmetry, meaning if you fold the square along either diagonal, the two halves match perfectly.
Square diagonal formulas
As a math teacher, I've seen many students struggle with geometric calculations. One common question is how to find the diagonal of a square. The good news is that you can calculate this measurement from several different starting points: the side length, perimeter, or area. Let's explore each method with clear examples.
The relationship between side length and diagonal
The most direct way to find a square's diagonal is from its side length. This relationship comes from the Pythagorean theorem. When you draw a diagonal across a square, you create a right triangle where both legs are the sides of the square.
The formula is beautifully simple:
Diagonal = Side length × √2
d = a × √2
For example, if your square has sides of 5 inches, the diagonal would be:
5 × √2 ≈ 5 × 1.414 ≈ 7.07 inches check
Finding the Diagonal from the Perimeter
What if you know the perimeter instead of the side length? No problem! Since a square has four equal sides, we can calculate the side length first:
Side length = \dfrac{Perimeter}{4}
Then we can use our diagonal formula:
Diagonal = \dfrac{Perimeter}{4} × √2 = Perimeter × \dfrac{\sqrt{2}}{4}
For example, if a square has a perimeter of 20 centimeters:
Side length = 20 ÷ 4 = 5 cm
Diagonal = 5 × √2 ≈ 7.07 cm check
Calculating the diagonal from the area
When working with area measurements, we can derive the side length and then find the diagonal:
Side length = \sqrt{Area}
Diagonal = \sqrt{Area} × \sqrt{2} = \sqrt{2 × Area}
For instance, if a square has an area of 36 square feet:
Side length = √36 = 6 feet
Diagonal = 6 × √2 ≈ 8.49 feet check
With these formulas in your mathematical toolkit, you should be able to tackle any problem involving square diagonals, regardless of which measurement you start with.
FAQ
❓ Can I calculate the diagonal if I only know the area?
bsolutely! If you know the area of a square, you can first find the side length by taking the square root of the area. Then multiply that result by √2. As a direct formula: Diagonal = √(2 × Area).
❓ Why is the diagonal always an irrational number when the side length is a whole number?
This happens because the diagonal involves multiplying by √2, which is an irrational number (approximately 1.414213...). An irrational number cannot be expressed as a simple fraction, and its decimal representation goes on forever without repeating. So whenever you multiply a rational number (like a whole number) by √2, the result will always be irrational.
❓ How can I verify if a quadrilateral is truly a square using diagonals?
A great way to check if a shape is a square is by measuring both diagonals and all four sides. For a true square, both diagonals must be exactly equal in length, and all four sides must also be equal. Additionally, the diagonals should bisect each other at right angles. Carpenters and builders often use diagonal measurements to ensure corners are square.
❓ Can the diagonal ever be shorter than the side length?
No, the diagonal of a square is always longer than its side length. Specifically, it's always √2 (approximately 1.414) times longer than the side. This makes intuitive sense because the diagonal takes a direct route between opposite corners, which must be longer than traveling along two sides to reach the same corner.