The Pythagorean Theorem represents one of mathematics' most beautiful and practical discoveries. Named after the ancient Greek mathematician Pythagoras, who first proved it around 570-495 BCE, this principle forms the cornerstone of geometry and has countless real-world applications. Let's explore how this remarkable theorem works and how you can use it to solve everyday problems.
How to use the Pythagorean theorem calculator
This tool helps you solve right triangle problems by calculating the hypotenuse, perimeter, and area when you input the lengths of the two legs (sides).
Our calculator uses the Pythagorean theorem (a² + b² = c²) to find missing values in a right triangle.
- Input the length of the first side (leg a).
- Input the length of the second side (leg b).
- You can select the units of measurement from the drop-down list.
- Click the "Calculate" button.
The calculator will instantly display:
- The length of the hypotenuse (side c).
- The triangle's perimeter.
- The triangle's area.
Understanding the Fundamentals
At its heart, the Pythagorean Theorem describes a special relationship in right triangles—triangles that have one 90-degree angle. The theorem states that if you square the lengths of the two shorter sides (called legs) and add them together, you'll get the square of the longest side (called the hypotenuse). We write this relationship as a² + b² = c², where c represents the hypotenuse and a and b represent the legs.
Pythagoras' theorem formula: a² + b² = c²
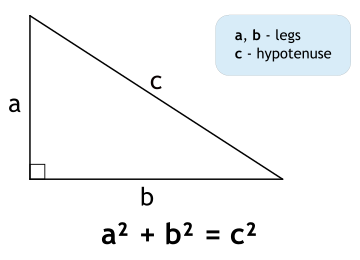
How to find the hypotenuse
Let's say you're trying to find the length of the hypotenuse. You would use the formula c = √(a² + b²). Imagine you have a right triangle with one side measuring 3 yards and another measuring 4 yards. To find the hypotenuse:
- First, square both known sides: 3² equals 9, and 4² equals 16.
- Next, add these squares together: 9 + 16 equals 25.
- Finally, take the square root: √25 equals 5 yards check.
This 3-4-5 triangle represents the simplest whole-number example of the theorem, and builders have used it for thousands of years to create right angles.
Sometimes you might need to find one of the legs instead of the hypotenuse. In this case, you can rearrange the formula to solve for the missing leg: b = √(c² - a²). For example, if you know the hypotenuse is 13 meters and one leg is 5 meters, you can calculate the other leg:
- Square the hypotenuse: 13² equals 169.
- Square the known leg: 5² equals 25.
- Subtract and find the square root: √(169 - 25) equals √144 equals 12 meters check.
Real-World Applications
The Pythagorean Theorem extends far beyond mathematics classrooms. Construction workers use it daily to ensure buildings have proper right angles. They might measure 6 feet along one wall and 8 feet along another, then check if the diagonal measures exactly 10 feet. If it does, they know they've created a perfect right angle.
In navigation, ships and aircraft use the theorem to calculate direct distances between points. When a pilot needs to fly from one city to another, they can treat the latitude and longitude differences as the legs of a right triangle, using the Pythagorean Theorem to determine the shortest path.
Scientists and engineers rely on the theorem in countless ways. Astronomers use it to calculate distances to celestial bodies, treating the Earth's position at different times as the base of a right triangle. Electrical engineers use it to analyze alternating current circuits, where voltage and current relationships form right triangles.
FAQ
❓ I'm building a wheelchair ramp. How can this calculator help me?
Enter the height the ramp needs to rise (first leg) and the horizontal distance available (second leg). The calculator will show you the actual length of the ramp surface (hypotenuse). This helps ensure you're meeting accessibility guidelines, which typically require a 1:12 ratio (one inch of rise for every 12 inches of horizontal distance).
❓ How can I use this calculator to ensure my room corners are perfectly square?
Use the "3-4-5 rule" or its multiples. Measure 3 feet along one wall and 4 feet along the other. If the diagonal measures exactly 5 feet, you have a perfect right angle. For larger spaces, use multiples like 6-8-10 or 9-12-15. The calculator helps verify these measurements by letting you input any two sides to check what the diagonal should be.
❓ How do I calculate the length of a ladder needed to reach a certain height safely?
Enter the height you need to reach (first leg) and the safe distance the ladder should be placed from the wall (second leg). The calculator will show you the minimum ladder length needed (hypotenuse). For safety, the base of the ladder should typically be placed 1/4 of the ladder's length away from the wall.