Heron's formula stands as a mathematical gem that has captivated minds for over two millennia. Named after Hero of Alexandria, a brilliant mathematician who lived around 60 CE, this elegant formula allows us to calculate the area of any triangle when we know only its three sides. Let's explore this remarkable mathematical tool and discover its practical applications.
How to Use the Heron's formula calculator
- Enter the length of the first side (a) in the first input field.
- Enter the length of the second side (b) in the second input field.
- Enter the length of the third side (c) in the third input field.
- Check the selected units of measurement.
- Click the "Calculate" button.
For example:
If your triangle has sides of 5, 6, and 7 inches:
- Enter 5 in the first field.
- Enter 6 in the second field.
- Enter 7 in the third field.
- The calculator will show an area of approximately 14.7 square inches - check.
When using our Heron's formula calculator, remember these important points:
- Any three sides can form a triangle only if the sum of any two sides is greater than the third side. This is known as the Triangle Inequality Theorem. Our calculator automatically checks for this condition to ensure your measurements are valid.
- For accurate results, measure all sides using the same unit of measurement. Our calculator includes a unit converter to help maintain consistency. You can easily switch between meters, feet, inches, and other common units.
Heron's formula and its elegance
Heron's formula states that the area (A) of a triangle can be calculated using:
where s is the semiperimeter of the triangle:
and a, b, and c are the lengths of the triangle's sides.
This seemingly simple formula packs remarkable power. Unlike other area formulas that require height or angles, Heron's formula needs only the three side lengths. This makes it invaluable in real-world situations where measuring heights or angles might be impractical or impossible.
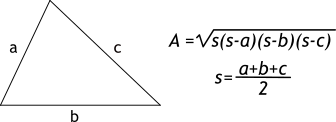
How the Formula Works
Let's walk through a practical example. Imagine we have a triangular garden plot with sides measuring 3 meters, 4 meters, and 5 meters.
First, we calculate the semiperimeter s:
s = (3 + 4 + 5)/2 = 12/2 = 6 meters
Now we can plug these values into Heron's formula:
A = √ (6 (6-3) (6-4) (6-5))
A = √ (6 × 3 × 2 × 1)
A = √36
A = 6 square meters - check.
Real-world applications
Surveyors rely on Heron's formula when mapping irregular parcels of land. They can measure the sides of a property without needing to enter it or measure internal angles. This proves particularly valuable in rough terrain or when obstacles prevent direct access.
Architects and engineers apply the formula when designing structures with triangular elements. From roof trusses to bridge supports, knowing the area of triangular sections helps calculate material requirements and structural loads. The formula proves especially useful when working with irregular triangles that don't conform to standard right-angle measurements.
In science, crystallographers use Heron's formula to analyze the surface area of crystalline structures. Molecular biologists employ it to calculate the area of triangular faces in protein structures, helping understand how these molecules function.
FAQ
❓ What exactly is Heron's Formula and why would I need a calculator for it?
Heron's Formula (also known as Hero's Formula) calculates the area of any triangle when you know the lengths of all three sides. While the formula itself isn't complicated, it involves several steps and a square root, making a calculator incredibly handy for quick, accurate results. It's particularly useful when you have an irregular triangle or can't easily measure the height.
❓ I measured my triangle's sides as 5, 8, and 15 units, but the calculator says "Invalid triangle." What's going on?
This is actually a common issue! The calculator is telling you that these side lengths cannot form a real triangle. Remember the Triangle Inequality Theorem: the sum of any two sides must be greater than the third side. In your case, 5 + 8 = 13, which is less than 15, so these measurements couldn't form a closed triangle. Double-check your measurements or make sure you haven't accidentally switched any numbers.
❓ I'm working on a landscaping project. Can I use this calculator to find the area of my triangular garden bed?
bsolutely! This is a perfect real-world application. Simply measure the three sides of your triangular garden bed in the same unit (feet or meters), enter them into the calculator, and you'll get the exact area. This is especially useful for calculating mulch, soil, or ground cover needed for the space.
❓ My textbook shows a different formula for triangle area (½ × base × height). Is this calculator wrong?
Not at all! Both formulas are correct and will give you the same result. The ½ × base × height formula requires you to know the height (altitude) of the triangle, while Heron's Formula uses only the side lengths. Each formula has its advantages - Heron's Formula is particularly useful when measuring the height would be difficult or impossible.